Warning: include(../box/CAcrypto.php): Failed to open stream: No such file or directory in /usr/local/var/www/source/CNDescriptors.php on line 34
Warning: include(): Failed opening '../box/CAcrypto.php' for inclusion (include_path='.:/usr/local/Cellar/php/8.4.1_1/share/php/pear') in /usr/local/var/www/source/CNDescriptors.php on line 34
Warning: include(../box/biodiversity.php): Failed to open stream: No such file or directory in /usr/local/var/www/source/CNDescriptors.php on line 38
Warning: include(): Failed opening '../box/biodiversity.php' for inclusion (include_path='.:/usr/local/Cellar/php/8.4.1_1/share/php/pear') in /usr/local/var/www/source/CNDescriptors.php on line 38
Warning: include(../box/admission.php): Failed to open stream: No such file or directory in /usr/local/var/www/source/CNDescriptors.php on line 42
Warning: include(): Failed opening '../box/admission.php' for inclusion (include_path='.:/usr/local/Cellar/php/8.4.1_1/share/php/pear') in /usr/local/var/www/source/CNDescriptors.php on line 42
Warning: include(../box/recentPapers.php): Failed to open stream: No such file or directory in /usr/local/var/www/source/CNDescriptors.php on line 46
Warning: include(): Failed opening '../box/recentPapers.php' for inclusion (include_path='.:/usr/local/Cellar/php/8.4.1_1/share/php/pear') in /usr/local/var/www/source/CNDescriptors.php on line 46
Warning: include(../box/random.php): Failed to open stream: No such file or directory in /usr/local/var/www/source/CNDescriptors.php on line 50
Warning: include(): Failed opening '../box/random.php' for inclusion (include_path='.:/usr/local/Cellar/php/8.4.1_1/share/php/pear') in /usr/local/var/www/source/CNDescriptors.php on line 50
Source Code: A complex network-based approach for boundary shape analysis

This page provides the source code for the complex network-based approach for boundary shape analysis. In pattern recognition and image analysis, shape is one of the most important visual attributes to characterize objects. It provides the most relevant information about an object in order to identify and classify tasks.
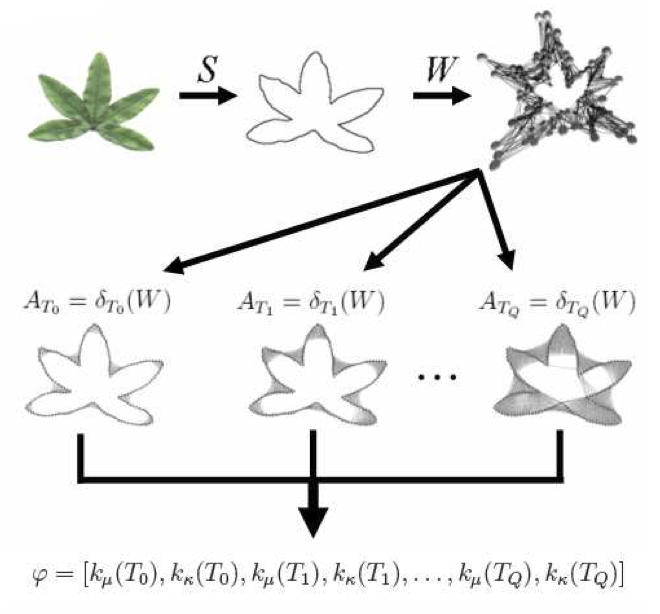
The method proposed here, has a novel approach to the shape boundary analysis using the Complex Networks Theory. It considers the shape boundary as a set of points and models this set as a graph. The topology of a Small World network model is obtained artificially by transformations on vertices of shape model. The topological features, derived from the dynamics of the network growth, are correlated to physical aspects of the shape. Consequently, these measurements can be used to compose a shape descriptor or signature. These descriptors may be used to identify and distinguish objects.
Traditional shape boundary methods yield the shape descriptors using the contour as continuous closed curves formed by the adjacent consecutive pixels. By modeling the shape boundary as complex network, the method proposed here, on the other hand, does not need adjacent and sequential pixels as the graph model only takes the distance between the boundary elements into account.
Main algorithm characteristics:
This method is one of the best performance methods to shape analysis. Besides its great performance, this method has also some interesting characteristics, that make it suitable for a wide range of applications:
-
Rotation invariant, since it is based on graphs.

-
Scale invariant. The method has an embedded scale normalization that makes it be naturally scale invariant.

-
Noise tolerance. The method has a good noise tolerance. Noise corrupted contours can be easily classified.

-
Contours with continuous degradation. This is the great advantage of this method. Most of the shape analysis algorithms deals with complete and not corrupted contours. This algorithm can characterize the contour even if it was degradate and most part of the contour is missing.

-
Contours with random degradation. This is the great advantage of this method. Most of the shape analysis algorithms deals with complete and not corrupted contours. This algorithm can characterize the contour even if it was degradaded and most part of the contour is missing. The degradation can be continuous or random.

Algorithm's concept:
The main idea of the algorithm is to obtain a feature vector that is capable to characterize the shape (last step of the diagram). The algorithm considers the shape boundary as a set of points and models it as a graph. The topological features, derived from the dynamics of the network growth, are correlated to physical aspects of the shape.
Source code:
The source code of the method is available under Creative Commons License. The source-code was written in Matlab, there is an example and demonstration of how to use it.
To receive the source code, please follow the link bellow and fill the form. It will be emailed to you.
![]()
![]()
![]() GET THE SOURCE CODE - click here
GET THE SOURCE CODE - click here ![]()
![]()
![]()
License:

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
How to cite this work:

If this work is helpfull to you or aided you to improove your research, please cite:
Backes, A. R., Casanova D. and Bruno, O. M. "A complex network-based approach for boundary shape analysis". Pattern Recognition, 42(1):54-67, 2009
To acess information about this paper access this link or do directly to the doi page:
 10.1016/j.patcog.2008.07.006
10.1016/j.patcog.2008.07.006
Source Code example and demonstration:
There are two .m files in the source code:
- CNDescriptors.m - Contains the function CNDescriptos which extracts features from the shape.
- cndExample.m - Demonstration of how to use the CNDescriptors function
The function works with black and white image (background in black / points of interest in white).
There are two ways of use the function CNDescriptos, the simplest one is using the image as argument, for example: descriptors = CNDescriptors(img), in this case, the function uses the default threshold. The threshold argument is optional, you can use your own parameter using, for instance, the vector t = 0.01:0.01:1 and calling the function with the threshold vector: descriptors = CNDesriptors(img, t).
To run the demonstration, just call the file cndExample.m. In this demo, there are load nine images grouped into thress classes: sample, square and triangle. The figure bellow shows the images (first row: sample, second row: triangle, and third row: square). As can be noticed the shapes are irregular and in different scales.
 |
 |
 |
| sample1 | sample2 | sample3 |
 |
 |
 |
| triangle1 | triangle2 | triangle3 |
 |
 |
 |
| square1 | square2 | square3 |
The demo, extracts a descriptor from each one of the images and plots a graph with them. In the first graph in the following, there are the original descriptors obtained from each image. Notice that the classes (plotted with the same color) are grouped into the plots. This way, the shapes could be easy recognized by a pattern recognition method. On the second graph, the plots are normalized by the equation of the straight line that crosses the descriptors. In the normalized plot, the characteristics of each class and how they are grouped are highlighted, make easy to observe the performance of the method.
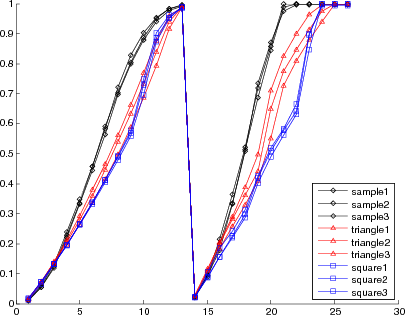
Descriptors obtained from each demonstration image
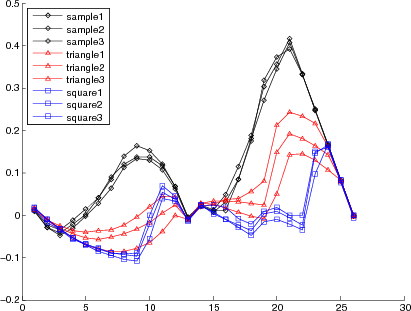
Normalized Descriptors from each demonstration image
Related work:
Text related to the source code.
