Cellular automata: formalism, stability and application portfolio

In this course an overview will be given of the modelling paradigms that are located at the discrete side of the spectrum of spatio-temporal models with particular emphasis on so-called cellular automata, which are mathematical models that are discrete in all their senses. Having introduced these paradigms, it will be shown how one can assess the stability of such models using similar tools as the ones used for characterizing continuous dynamical systems. Finally, the benefits of discrete modelling paradigms for setting up trustworthy in silico experiments will be demonstrated.

dr. ir. Jan Baetens

Department of Mathematical Modelling, Statistics and Bioinformatics

Ghent University

Course material

Cellular automata and beyond

Stability properties of cellular automata

Application portfolio

dr. ir. Jan Baetens

Department of Mathematical Modelling, Statistics and Bioinformatics

Ghent University

Cellular automata examples

An ever increasing amount of Internet resources is available on spatio-temporal models, especially on the utter discrete paradigm, e.g. cellular automata, which have known a true revival following Stephen Wolfram's magnum opus. Much less well-known are various types of mathematical models which are somewhere in between PDEs and CA which are at the extremes of the spectrum of mathematical models available for spatio-temporal modelling. For instance, coupled-map lattices share discreteness of time and space with CA, though can take arbitrary state values like PDEs.

Partial differential equations

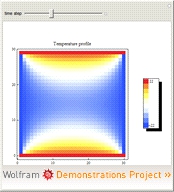
PDEs are at the continuous extreme of the earlier mentioned model spectrum, and are the tool par excellence to solve numerous engineering problems. They have been long- and well-studied as extensions of ordinary differential equation for spatio-temporal evolving phenomena which is most often resorted for solving engineering problems. For that reason, several PDEs have been named due to their frequent use in various scientific domains, such as the heat equation, the diffusion equation, and so on. Numerous textbooks have been published on the topic, which are already covered by (advanced) courses offered at most engineering and science faculties.

Figure 2: final temperature distribution modelled by means of the 2D heat equation

As an example, Figure 2 shows the steady-state temperature distribution in initially cold room (blue) which is heated through heating elements installed in the floor and ceiling of the room.

Cellular automata

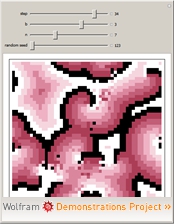
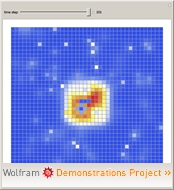
A cellular automaton is at the other end of the earlier mentioned model spectrum, being discrete in all its senses, e.g. space is represented by an infinite lattice of cells, updates occur only at discrete time steps and the states can only take a finite number of values. CA were first introduced by John von Neumann and Stanislaw Ulam as `cellular spaces', and later on explored in detail by Stephen Wolfram who postulated that only four different classes of CA-behaviour would exist which has not been countered until now. According to this classification, CA can evolve

• homogeneous patterns
• periodic, nested structures
• chaotic patterns
• local, persistent structures

(a)	(b)
(c)	(c)
Figure 3: possible CA-behaviour: homogenous (a), nested (b), chaos (c) and persistent structures (d)

In addition to this classification scheme, Wolfram proposed an enumeration scheme for regular CA, enabling researchers to communicate about these models conveniently. Although some CA were found to evolve patterns which resemble patterns we can observe in nature, emphasis of CA-research was on the fundamentals of these CA rather than on their applicability outside this mathematical subdiscipline. As such, much attention has been paid to CA capable of universal computation, reversible CA, and so on. The two-dimensional CA, named the Game of Life is probably the most well-known CA originating from this fundamental research. From a more practical viewpoint, CA have been found which generate patterns that are qualitatively alike to patterns arising from everyday natural processes such as, forest fires, animal migration, crystal formation, and so on.

In addition to this classification scheme, Wolfram proposed an enumeration scheme for regular CA, enabling researchers to communicate about these models conveniently. Although some CA were found to evolve patterns which resemble patterns we can observe in nature, emphasis of CA-research was on the fundamentals of these CA rather than on their applicability outside this mathematical subdiscipline. As such, much attention has been paid to CA capable of universal computation, reversible CA, and so on. The two-dimensional CA, named the Game of Life is probably the most well-known CA originating from this fundamental research. The evolution of this CA, which is computational irreducible and capable of universal computation, from random initial conditions is depicted in Figure 4. From a more practical viewpoint, CA have been found which generate patterns that are qualitatively alike to patterns arising from everyday natural processes such as, forest fires, animal migration, crystal formation, and so on.

Contributions to the Wolfram Demonstrations Project

Lyapunov exponents of elementary cellular automata	Sensitivity of elementary cellular automata to their unputs
CCA for steady-state heat flow	Greenberg-Hastings model
Mimicking the Kuramoto-Sivashinsky equation using cellular automaton

Further reading

There's a rich variety of books and Internet resources on CA and other types of spatio-temporal models from which I list the most illustrative below.

• Ilachinski, A. (Ed.), 2001. Cellular Automata. A Discrete Universe. World 168 Scientific, London, United Kingdom.
• J.L. Schiff. Cellular Automata: A Discrete View of the World. John Wiley & Sons Ltd., Chichester, United Kingdom, 2008.
• T. Tyler, Cellular Automata tutorial
• S.Wolfram. Statistical mechanics of cellular automata. Reviews of Modern Physics, 55:601-644, 1983
• S. Wolfram, editor. A New Kind of Science. Wolfram Media Inc., Champaign, United States, 2002.
• S. Wolfram, WolframScience