LLNA: Life-like Network Automata
Gisele Helena Barboni Miranda , Jeaneth Machicao
, Jeaneth Machicao , Odemir M. Bruno
, Odemir M. Bruno 
The Life-Like Network Automata (LLNA) was designed for pattern recognition in networks. LLNA uses the network topology as the tessellation of a Cellular Automata (CA), whose dynamics produces a spatio-temporal pattern used to extract the attributes for network characterization. The implemented CA is inspired by the rules of Life-Like as illustrated below. LLNA is a good choice for pattern recognition applications using networks and demonstrates potential for general applicability. The reader can found more details at references:
- Miranda, G. H. B., Machicao, J. and Bruno, O. M. Exploring spatio-temporal dynamics of cellular automata for pattern recognition in networks. Scientific Reports 6, 37329 (2016)
- Machicao, J., Corrêa Jr E. A., Miranda, G. H. B., Amancio, D. R. and Bruno, O. M. Authorship attribution based on Life-like network automata. ArXiv e-prints 1610.06498 (2016)
The figure below presents an overview of LLNA.
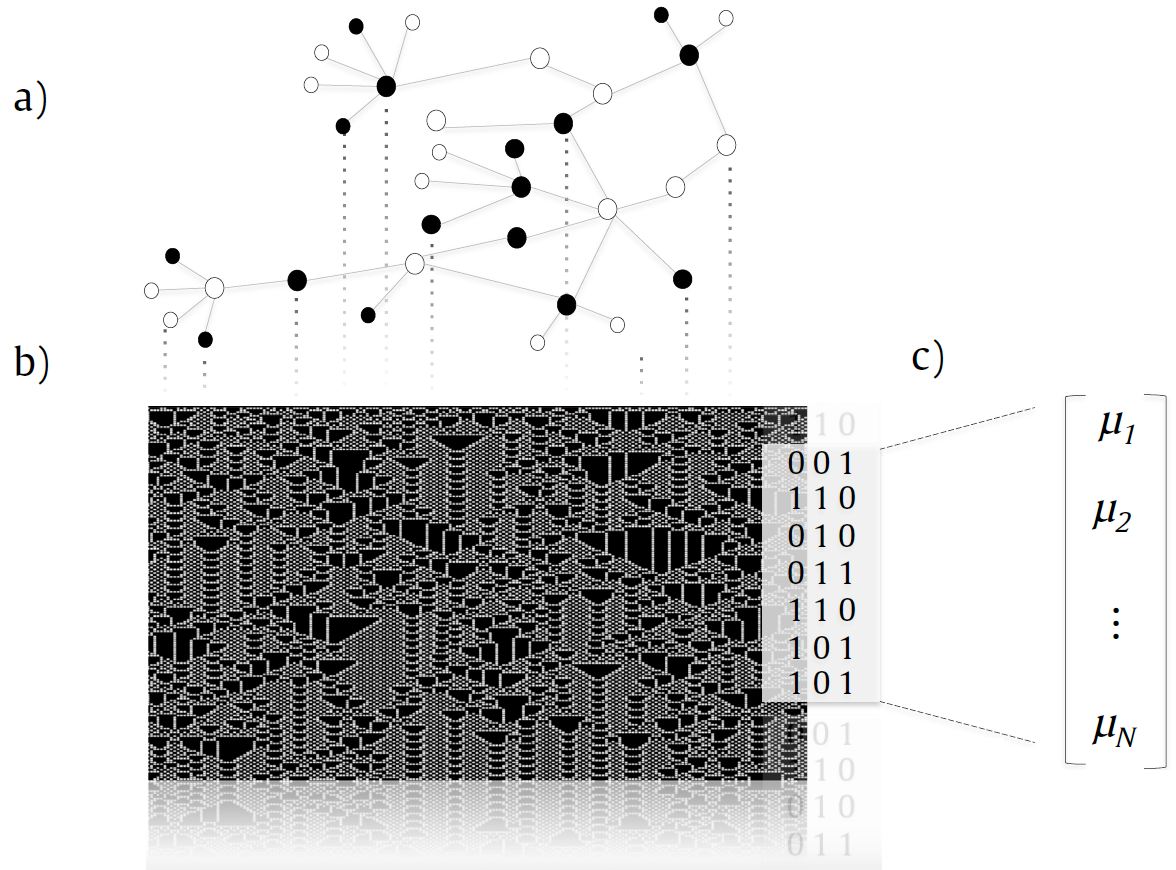
LLNA
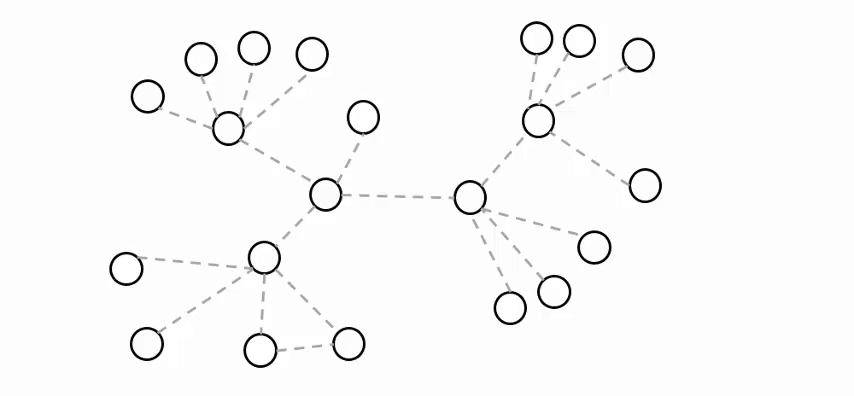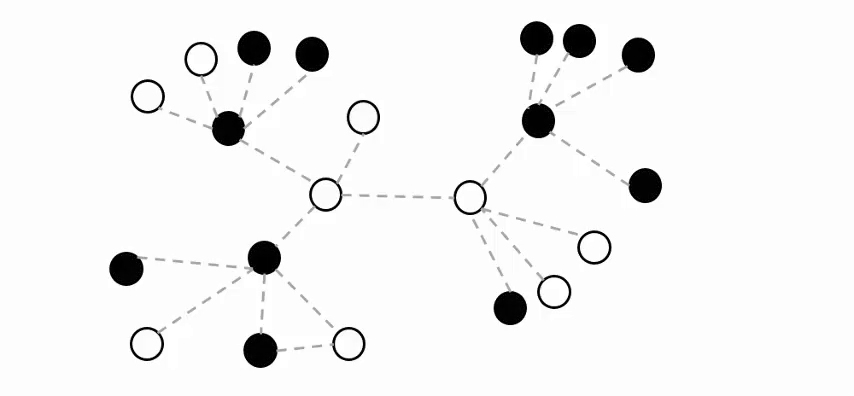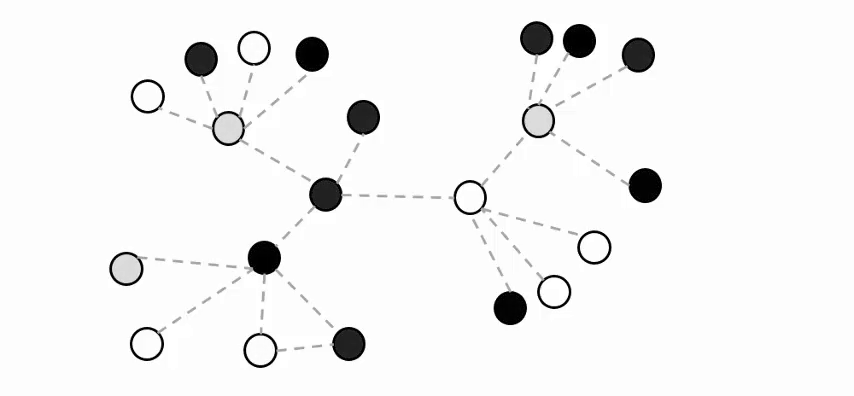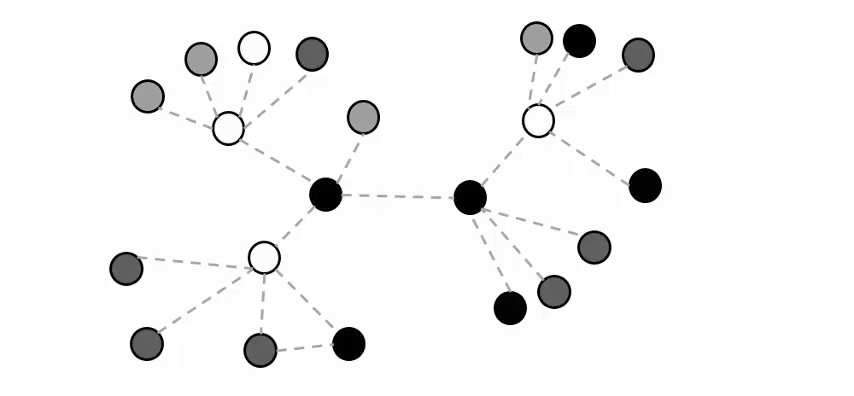 |
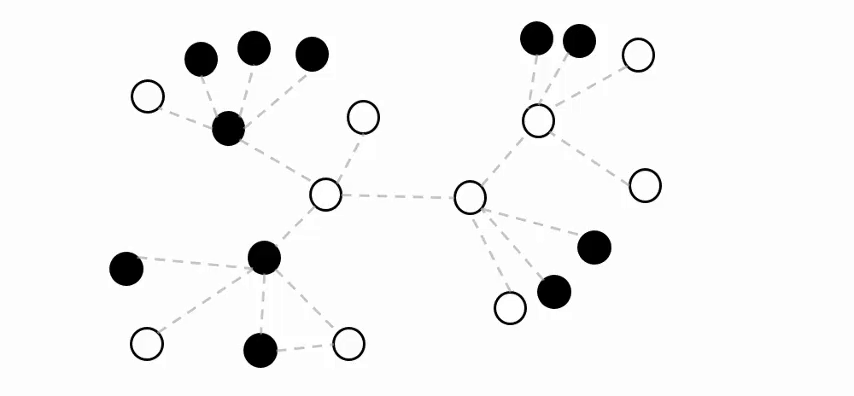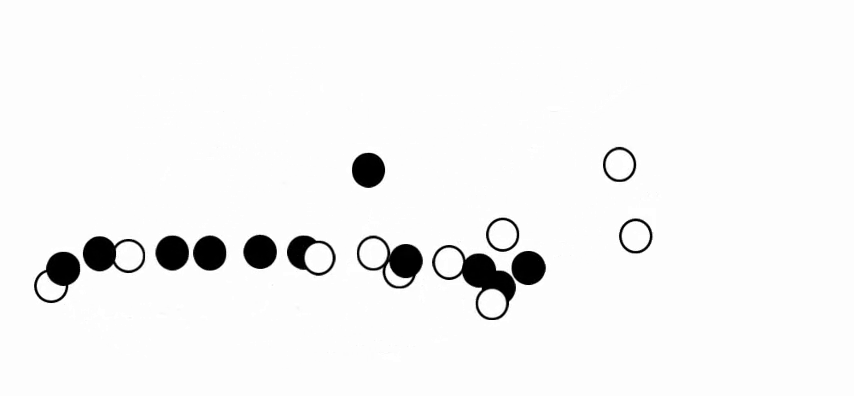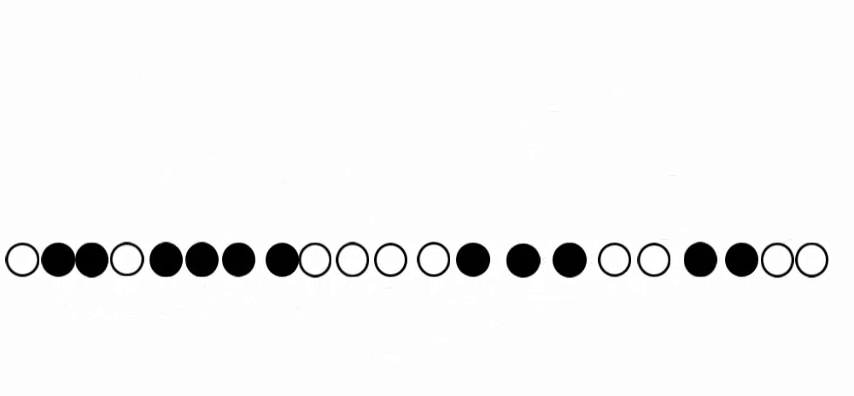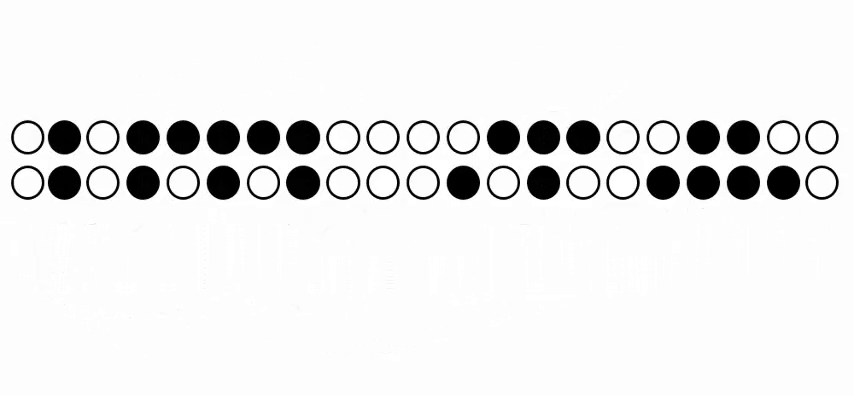
a) Modeling a binary cellular automaton over the network topology. Black cells represent the nodes in the ``on'' state and white cells, the nodes in the ``off'' state. |
 |
b) Spatio-temporal diagram of the evolved automaton. Each column of the diagram represents the evolution of a single node and each row represents the configuration of the states at each time step. |
 |
c) Network descriptor represented by a vector of attributes obtained from the previous diagram. |
LLNA Demo
Datasets
Synthetic dataset
Composed of synthetic networks generated according to the following models: (i) Random; (ii) Small-world, with rewiring probability of $p=0.1$; (iii) Scale-free, with both linear and non-linear preferential attachment, and, (iv) Geographical. For each model, there are networks with the following values of mean degree (
Synthetic scalefree dataset Composed of scale-free networks generated according to the models proposed by Barabasi & Albert [1] and Dorogovtsev & Mendes [2]. For the first model, we generated networks with the following values of power law exponent ($\gamma$): 0.5, 1.0, 1.5 and 2.0. Therefore, we have five classes in this dataset, the four different $\gamma$ exponent networks and the networks generated through the second scale-free model. The dataset contains 100 networks for each of these five classes with $N = 1000$ nodes and $\langle k \rangle=8$. Download here
[1] Barabasi, A.-L. & Albert, R. Emergence of scaling in random networks. Science 286, 509-512 (1999).
[2] Dorogovtsev, S. N. & Mendes, J. F. Evolution of networks. Adv. Phys. 51, 1079-1187 (2002).
